

原来(8×8×1)的长方体和拼成的(4×4×4)的立方体如下图所示(仅作示意):
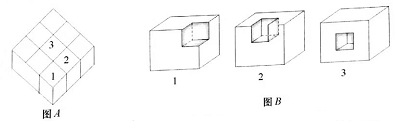
如图A所示,原来的长方体有三种方块,我们标记为:A1—有4个面涂黑;A2—有3个面涂黑;A3—2个面涂黑。
如图B所示,新拼的立方体有四种方块,我们标记为:B1—在角上,有3个面外露;B2—在棱上,有2个面外露;B3—在侧面中,有1个面外露;B4—在中心,没有面外露,图中看不到。
经过计算,可知各个方块数目如下:

题目要求黑色的面尽量外露,我们统筹安排,让A3去填充B3和B4(还剩4块A3),让A2去填充B2(没有剩余),让A1去填充B1(还缺4块)。最后让剩余的4块A3去填充B1,只有这4块会有白色表面外露,每块有2个白色的表面外露,共8个白色的表面外露。立方体总外表面积为4×4×6=96(平方厘米),所以外表面为黑色的面积有96-8=88(平方厘米)。
故选A。
