

一、情景引入
某天,有两个小朋友得到了一块三角形蛋糕,他们决定把它平分吃掉,你能帮他们解决这个问题吗?若又来了两个人呢?
从三角形的中线引入到三角形的中位线
可以和三角形的中线比较,加深认识。
二、探索新知
(1)让学生自己动手画一条三角形的中位线,通过观察、测量,猜测三角形中位线的性质,并让学生把发现的规律用命题形式表示出来。
让学生亲身经历通过观察、实验等数学活动,发现数学的过程,这对培养学生发现问题和提出问题的能力有着重要意义。
(2)证明三角形的中位线定理
此处证明经验较少,难度较高,可以提示学生从线段倍分转化为相等作为突破口,逐渐引导到利用平行四边形的相关知识解决问题。
(3)定理总结
展示三角形的中位线定理用几何语言如何表述,以及探讨定理有哪些用处。
三、巩固练习:智力过三关
如图,在△ABC,D,E,F分别是AB,AC,BC边上的中点。
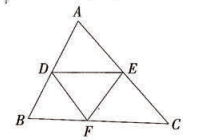
(1)若BC=8cm,则DE=_____cm。
(2)若△ABC的周长为18cm,则△DEF的周长为______cm。
(3)图中有_____个全等三角形,有_____个平行四边形,若△ABC的面积为36cm²,则△DEF的面积为______cm²。
通过三个题目练习加深对三角形中位线定理的认识,由学生表述理由,可以锻炼口头表达能力。
四、综合应用和知识拓展
(1)任意画一个四边形,顺次连接四边中点,得到一个什么四边形?
(2)证明中点四边形是一个平行四边形。
定理学习的一般环节:①了解定理的内容,能够解决什么问题(情境引入中体现);②理解定理的含义,认识定理的条件和结论,如在公式推导过程中对条件引起注意,通过对结论从结构,功能,性质,使用步骤等角度分析以加深印象和理解(探索新知中体现);③定理的证明或推导过程:学生与老师一起研究证明方法,如不需要证明,学生根据老师提供的材料体会定理规定的合理性(探索新知中体现);④熟悉定理的使用。循序渐进地应用定理,将定理纳入到已有的知识体系中取(巩固练习中体现);⑤引申和拓展定理的运用(知识拓展中体现)。
初中阶段的数学命题包括公理、定理、公式、性质和法则等。其教学过程分为命题引入、命题证明、命题巩固及命题应用四个阶段。因此该题目的教学设计应分为上述四个过程。
(1)命题引入:观察、实验的方法引入命题;观察、归纳的方法引入命题;由实际的需要引入命题。
(2)命题证明及命题明确.
(3)命题巩固:当堂巩固和及时复习两种方式。
(4)命题应用。安排好各类习题,既有基本训练题,又有巩固知识的题型,还要有综合型的题目。
具体为:
一、情景引入
某天,有两个小朋友得到了一块三角形蛋糕,他们决定把它平分吃掉,你能帮他们解决这个问题吗?若又来了两个人呢?
从三角形的中线引入到三角形的中位线
可以和三角形的中线比较,加深认识。
二、探索新知
(1)让学生自己动手画一条三角形的中位线,通过观察、测量,猜测三角形中位线的性质,并让学生把发现的规律用命题形式表示出来。
让学生亲身经历通过观察、实验等数学活动,发现数学的过程,这对培养学生发现问题和提出问题的能力有着重要意义。
(2)证明三角形的中位线定理
此处证明经验较少,难度较高,可以提示学生从线段倍分转化为相等作为突破口,逐渐引导到利用平行四边形的相关知识解决问题。
(3)定理总结
展示三角形的中位线定理用几何语言如何表述,以及探讨定理有哪些用处。
三、巩固练习:智力过三关
如图,在△ABC,D,E,F分别是AB,AC,BC边上的中点。
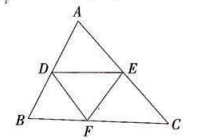
(1)若BC=8cm,则DE=_____cm。
(2)若△ABC的周长为18cm,则△DEF的周长为______cm。
(3)图中有_____个全等三角形,有_____个平行四边形,若△ABC的面积为36cm²,则△DEF的面积为______cm²。
通过三个题目练习加深对三角形中位线定理的认识,由学生表述理由,可以锻炼口头表达能力。
四、综合应用和知识拓展
(1)任意画一个四边形,顺次连接四边中点,得到一个什么四边形?
(2)证明中点四边形是一个平行四边形。
定理学习的一般环节:①了解定理的内容,能够解决什么问题(情境引入中体现);②理解定理的含义,认识定理的条件和结论,如在公式推导过程中对条件引起注意,通过对结论从结构,功能,性质,使用步骤等角度分析以加深印象和理解(探索新知中体现);③定理的证明或推导过程:学生与老师一起研究证明方法,如不需要证明,学生根据老师提供的材料体会定理规定的合理性(探索新知中体现);④熟悉定理的使用。循序渐进地应用定理,将定理纳入到已有的知识体系中取(巩固练习中体现);⑤引申和拓展定理的运用(知识拓展中体现)。
